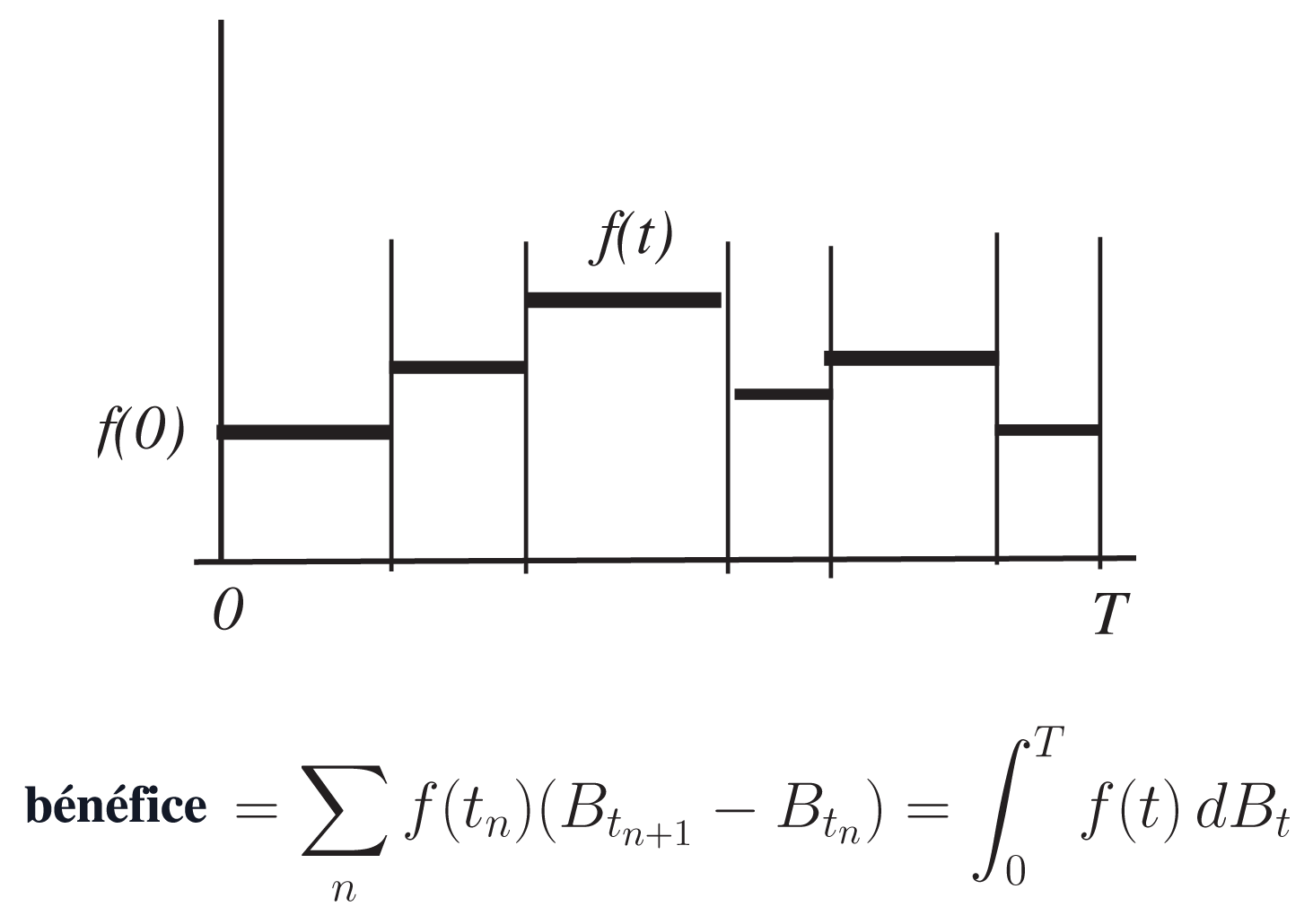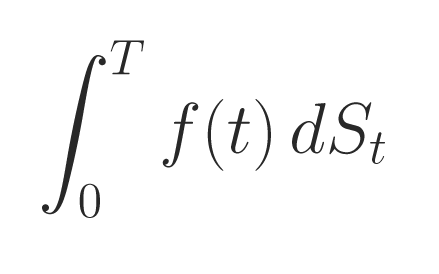Mathématiques financières, un aperçu

L’engouement parmi les chercheurs et les jeunes scientifiques depuis une trentaine d’années pour les mathématiques financières est certainement induit par le néolibéralisme dominant et l’influence progressive des marchés financiers sur les décisions de toutes sortes. Il n’en reste pas moins qu’il existe une articulation réelle entre certains concepts mathématiques — relativement avancés découverts au milieu du 20ème siècle — et la pratique financière. Cet accrochage doit être connu si l’on entend discuter cette situation plus à fond.

Je présente ici cette articulation le plus simplement possible selon le plan suivant

I. De Bachelier à Black-Scholes

II. La couverture des options : une nouvelle logique de gestion des risques financiers

III. Divers types de spéculation

Pour une introduction encore moins technique et d’orientation plus économique je renvoie à mon livre Martingales et marchés financiers, O. Jacob 1998, et pour une présentation mathématique claire des éléments essentiels à Lamberton D. et Lapeyre B., Introduction au calcul stochastique appliquée à la finance Ellipses 1992.

I. De Bachelier à Black-Scholes

Une notion fondamentale en calcul des probabilités — et maintenant en analyse — est la notion de martingale.

L’étymologie du mot vient de la ville de Martigues dont les habitants avaient certains usages vestimentaires. De là il est passé au vocabulaire des jeux de hasard et d’argent où il désigne une botte secrète. On explique dans les cours d’initiation aux probabilités que toutes ces « martingales des joueurs » ont un défaut et conduisent à la ruine.

L’emploi de ce terme en mathématiques est dû à Jean Ville[1] puis J. L. Doob. Il y désigne non une stratégie mais une catégorie de processus aléatoires. Une martingale est un processus dont la valeur actuelle est l’espérance conditionnelle (sachant une certaine « information ») des valeurs à une date ultérieure.

Les trajectoires des martingales ont des propriétés remarquables qui sont à l’origine de beaucoup de théorèmes profonds en divers domaines des mathématiques. Par exemple elles convergent (en un certain sens) lorsque le temps décroît vers t vers leur valeur en t.

Pour faire entrevoir ces propriétés de convergence considérons le cas où l’information est donnée par le partage de [0,1] en intervalles dyadiques de plus en plus fins. Les espérances conditionnelles ont alors l’allure suivante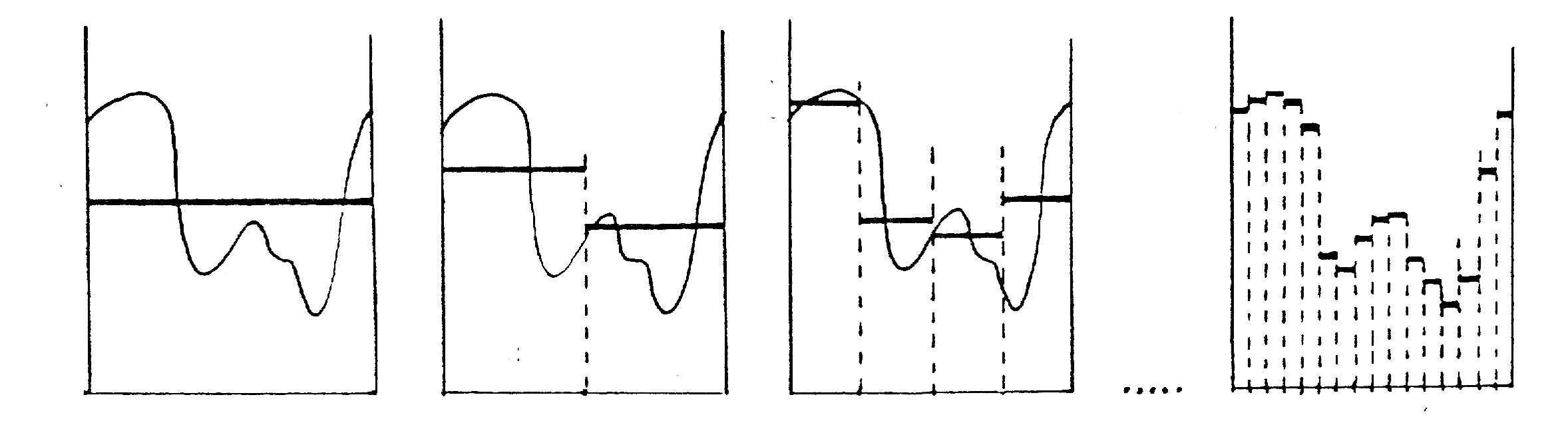

Une de leurs propriétés très significative pour les jeux de hasard est donnée par le théorème d’arrêt de Doob qu’on peut énoncer ainsi : à un jeu de hasard équilibré (où l’espérance de gain du joueur à chaque partie est nulle) le nombre de parties étant fini et fixé, si on quitte le jeu à un instant qui dépend du hasard du jeu alors l’espérance de gain est toujours encore nulle.

Mais bien avant que la notion de martingale soit explicitée, au début du 20^ème siècle, donc avant même que le calcul des probabilités ait pris la force et la rigueur que lui a donné Kolmogorov, Louis Bachelier, un précurseur de l’étude des processus à temps continu, s’était intéressé à la bourse. En termes modernes la vision que Bachelier avait des cours de bourses était celle d’un mouvement brownien centré, autrement dit d’une martingale gaussienne d’espérance constante. Il écrit « la bourse ne croit ni à la hausse ni à la baisse ». Son travail, connu de Kolmogorov, a été redécouvert par les économistes dans les années 1970.

Nous venons de prononcer le terme de mouvement brownien qui est une notion tout à fait centrale aussi bien en physique (Einstein et Smoluchovski (1906), Jean Perrin et Léon Brillouin, etc.) qu’en mathématiques où il fut étudié en premier lieu par Norbert Wiener au début des années 1920.

Faisons ici une parenthèse pour deux remarques intéressantes en philosophie des sciences à propos de ces idées de Wiener. D’abord le fait tout à fait extraordinaire que Wiener a dégagé un grand nombre de propriétés de la loi de probabilité du mouvement brownien (la mesure de Wiener) qui étendait la théorie de la mesure de Lebesgue au cas d’un espace de dimension infinie en 1921-23, et a été aussi en 1924 l’auteur d’un des progrès majeurs de la théorie du potentiel (sur la résolution du problème de Dirichlet) sans percevoir la connexion entre ces deux domaines de recherche, connexion qui sera découverte en 1944 indépendamment par Kakutani et Paul Lévy et donnera lieu à un immense courant d’investigation ouvrant la voie à toute l’analyse stochastique. Cette période peut être schématisée ainsi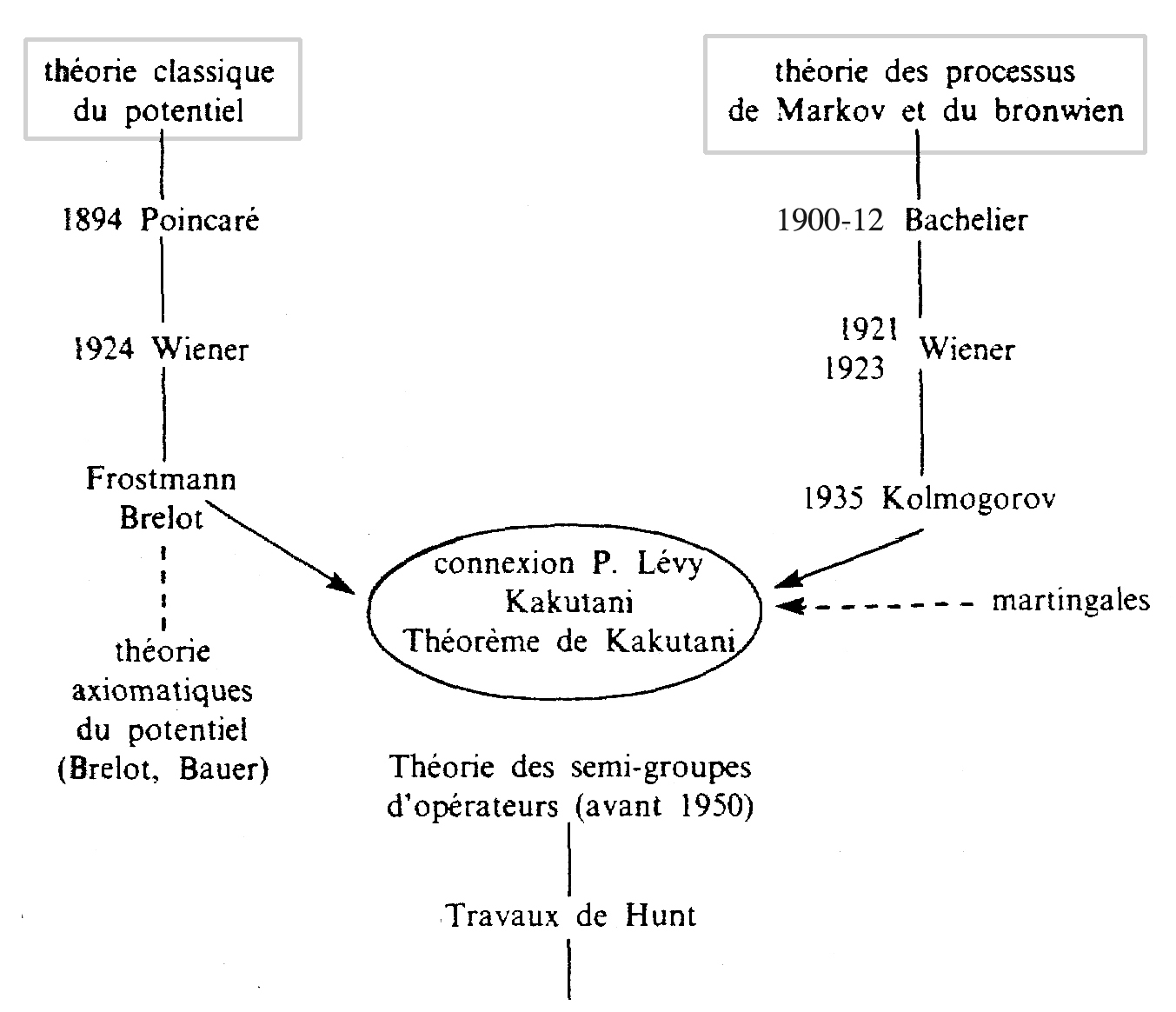

Par ailleurs, autre phénomène assez fréquent dans l’histoire des mathématiques, Wiener dégage en 1938 une décomposition orthogonale de l’espace du mouvement brownien, qu’il appelle les chaos, passée relativement inaperçue, qui sera à l’origine de développements passionnants dans la seconde moitié du 20^ème siècle avec notamment ce que l’on appelle le calcul de Malliavin et qui ont fait dire à Paul-André Meyer « L’intérêt est assez difficile à prévoir, les chaos de Wiener, par exemple, ont été découverts par Wiener dans les années 30, il en a donné la définition et personne ne s’y est intéressé… On prend conscience du fait qu’une chose qui n’a l’air de rien du tout est la clef, l’idée autour de laquelle toute sorte de choses s’organisent… »[2]

Après la guerre, l’intégrale stochastique qui avait été inventée par Wiener pour représenter les processus stationnaires et élaborer une théorie de Fourier aléatoire, fut étendue par Kiyoshi Itô au cas des martingales puis à d’autres processus aléatoires très généraux par tout un courant de chercheurs sous l’impulsion principale de Paul-André Meyer en un outil puissant appelé le calcul stochastique.

C’est dans ce langage que la finance va trouver de nouvelles représentations pertinentes (à la plus grande surprise de Itô lui-même).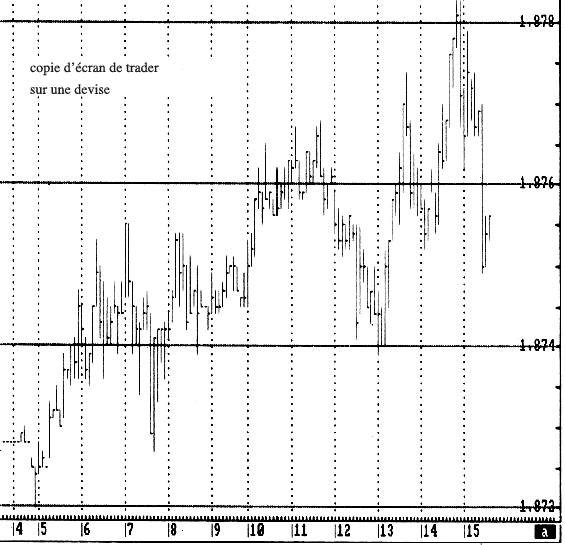

 

L’intégrale stochastique comme bénéfice du trader

Prenons le cas du modèle de Bachelier, le raisonnement est en fait très général. Le cours de l’actif est B_t  nous oublions pour simplifier les taux d’intérêt et l’actualisation.

Si à l’instant 0 le trader achète 1 unité et la revend à l’instant 1 son bénéfice est B₁–B₀.

Si à l’instant 0 le trader achète f(0) unités et les revend à l’instant 1 son bénéfice est de f(0)(B₁–B₀).

Si à l’instant 0 le trader achète f(0) unités et puis procède à des achats et des ventes de sorte qu’il possède f(t_n) unités durant l’intervalle de temps (t_n, t_n+1) et qu’il vend tout finalement, son bénéfice est de

Σ_n f(t_n)(B(t_n+1)-B(t_n))

Plus généralement si le trader s’arrange pour posséder f(t) unités à l’instant t son bénéfice final est donné par une intégrale par rapport au cours de l’actif.

L’idée s’étend au cas où la fonction f est générale grâce à l’intégrale de Wiener, et même au cas où elle dépend du hasard du cours jusqu’à l’instant présent, grâce à l’intégrale de Itô.

On voit que le calcul stochastique dont nous parlions intervient très naturellement, notons que ce calcul ne vérifie pas les formules de changement de variables habituelles mais la fameuse formule de Itô qui s’écrit (dans le cas de processus continus) :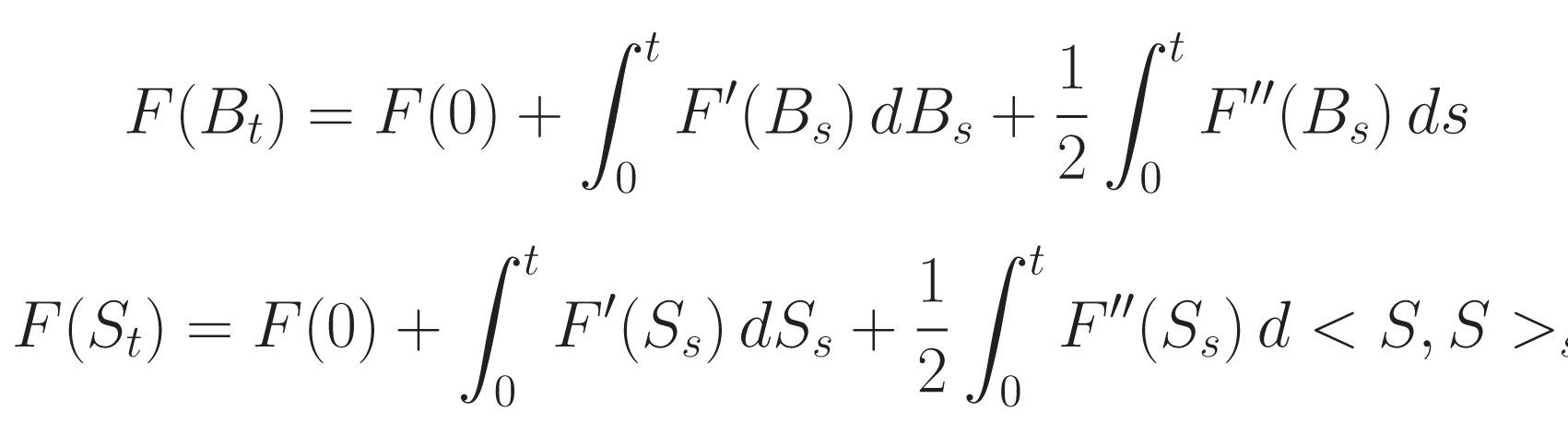

Nous pouvons résumer en disant que, si le cours de l’actif est S_t (processus aléatoire général appelé semi-martingale) et si le trader a constitué un portefeuille de f(t) actifs durant l’intervalle de temps (0, T), (sans anticiper sur les valeurs futures qu’il ne connaît pas) alors son bénéfice final s’écrit comme l’intégrale stochastique

II. La couverture des options : une nouvelle logique de gestion des risques financiers

Nous oublions toujours l’actualisation pour simplifier. Une option est dans le cas le plus simple d’un call un contrat, généralement passé entre une banque et un agent, autorisant ce dernier à acheter un actif financier (appelé le sous-jacent) à une date donnée T à un prix donné. L’agent peut alors à la date T profiter de cet avantage si le cours réel est plus élevé que le prix donné, ou ne pas exercer son droit si le cours est plus bas. Des options plus compliquées existent où l’on peut exercer son droit à tout instant jusqu’à T, et plus généralement on peut appeler option tout actif contingent dont la valeur dépend de l’évolution du cours entre maintenant et T.

Si le cours est un processus aléatoire S_t du style de ceux pour lesquels le calcul stochastique s’applique, on peut définir mathématiquement beaucoup d’actifs contingents avec les outils de l’espérance conditionnelle ou de l’intégrale stochastique.

Supposons qu’un actif contingent H puisse s’écrire de la façon suivante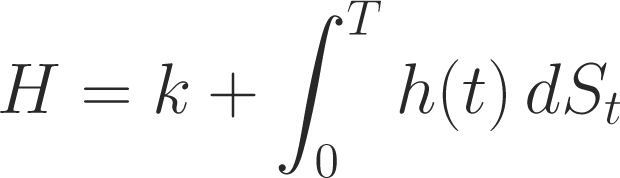

 

où h(t) est une fonction aléatoire non anticipante (celles avec lesquelles l’intégrale stochastique est définie) alors nous pouvons démontrer que l’avantage de disposer de H à l’instant T a un juste prix et que ce prix est k.

C’est le fameux raisonnement par absence d’arbitrage. Juste prix signifie que pour toute autre valeur soit l’acheteur soit le vendeur peut faire un profit sans risque.

En effet, raisonnons dans le cas où une banque vend cet actif contingent à un agent. Si la banque le vend k-ε, l’agent en construisant un portefeuille avec h(t) actifs à l’instant t réalisera, comme nous l’avons vu plus haut un bénéfice égal à l’intégrale stochastique de la formule ci-dessus et comme il a dépensé k-ε, il est en situation de réaliser un bénéfice total égal à ε sans risque. Si la banque vend l’actif contingent k+ε, c’est elle qui peut réaliser le profit ε.

Notons en revanche que si la banque vend l’actif contingent au prix k, la somme qu’elle aura à fournir à l’échéance T est aléatoire, mais elle dispose d’un moyen pour la fournir exactement sans dépenser finalement plus que la somme qu’elle a reçue c’est à dire k. Il lui suffit pour cela de constituer elle-même le portefeuille avec h(t) actifs au temps t.

Ceci est ce qu’on appelle la couverture en delta neutre, ou encore la couverture par simulation, elle nécessite beaucoup d’achats et de ventes durant l’intervalle (0,T) pour réaliser l’intégrale stochastique visée.

La mise en œuvre concrète de cette idée pour fixer le prix des actifs contingents suppose que l’on connaisse le processus aléatoire S_t. Là intervient la modélisation. La façon la plus simple, et encore la plus employée sur les marchés financiers, consiste à représenter l’actif avec un seul paramètre la volatilité à partir d’un mouvement brownien. C’est le modèle de Black-Scholes (1973).

C’est une hypothèse forte par rapport à la réalité observée, mais elle a l’avantage de la simplicité. Dans ce modèle on peut montrer que tout actif contingent s’écrit de cette façon

 

de sorte que le raisonnement par absence d’arbitrage permet de donner un prix à tous les produits dérivés. Les formules sont explicites dans le cas d’options simples pour trouver k et h(t) à partir de H on n’a qu’à résoudre une équation aux dérivées partielles elliptique en dimension 2.

Pour d’autres modèles (actifs avec sauts etc.) le marché est dit incomplet et la couverture de certaines options laisse des risques résiduels.

On voit que cette façon de gérer des actifs risqué avec un portefeuille de couverture est très différente de la façon classique qui était employée avant la « révolution Black-Scholes » et qui consistait à se faire une idée de la loi de probabilité qu’aura l’actif à la date T et de prendre l’espérance de la valeur de l’actif contingent. C’est ainsi qu’on avait procédé depuis la naissance des options au 19^ème siècle sur le marché des céréales.

C’est une logique différente qui est à l’œuvre ici, qui est aussi plus précise et qui favorisa incontestablement l’essor des marchés financiers dans les années 1970-80, début de la période dite néolibérale. Ainsi on a vu la naissance du LIFFE à Londres en 1982, du SIMEX à Singapour en 1974, di TIFFE à Tokyo en 1985, du MATIF à Paris en 1986, puis la création d’EURONEXT en 2000, etc.

Pour bien marquer cette différence, disons que l’ancienne logique est fondée sur l’espérance mathématique (moindres carrés) grâce aux savoirs d’experts (les ingénieurs qui travaillaient dans les banques pour estimer les risques des monnaies et des entreprises), elle accorde une valeur absolue aux « fondamentaux » de la réalité économique sous-jacente. Au contraire la nouvelle logique n’est pas fondée sur un principe d’assurance, elle procède client par client, elle est de domaine public, elle considère que les vrais prix sont ceux du marché et que les interprétations de politique économique sont subjectives.

III. Divers types de spéculation

Un marché permet la spéculation si on a la possibilité d’acheter et de revendre à tout moment un bien coté. C’est ce que font les marchés financiers. Notons que ce n’est pas le cas de tous les marchés, le marché de l’emploi, par exemple n’est pas de ce type, ni d’ailleurs les marchés sur lesquels raisonnaient Walras ou Jevons au 19ème siècle.

La spéculation économique est celle qui procède d’interprétations des évolutions des politiques et stratégies des firmes et des Etats. Elle concerne des échéance de l’ordre du mois où au delà où la réalité économique a changé. Elle est théorisée dans les manuels en disant que le spéculateur prend sur lui des risques dont les autres ne veulent pas.

La spéculation psychologique est beaucoup plus rapide et tente de tirer avantage du fait que les opérateurs sont des humains et donc enclins à interpréter certains phénomènes comme des indicateurs, des indices, et vont suivre avec une certaine grégarité les commentateurs et les rumeurs.

Enfin, et c’est une conséquence de l’hyper-mathématisation, il existe aussi une spéculation purement mathématique, qui tire parti notamment de non linéarités dans les transformations probabilistes, ou de perfectionnement de modèles épousant mieux la réalité observée.

Le trait le plus frappant de cette nouvelle finance mathématisée est certainement qu’elle est beaucoup plus loin du terrain, plus tournée vers ses propres procédures et son informatique, plus mondialisée aussi évidemment.

Les raisonnements par absence d’arbitrage sont assez convaincants pour ce qui est de l’agissement d’un agent individuel dans un marché existant mais ils ne nous renseignent pas sur la façon qu’a le marché lui-même d’obtenir l’information économique pertinente. La gestion des risques par portefeuille simulant telle que nous l’avons exposée ci-dessus renforce le fait que les marchés financiers sont très fortement autoréférentiels, chacun agit comme si les autres savaient. Ceci est une des causes des instabilités globales et cela entraîne une moins bonne allocation des ressources.

Si un agent économique est prêt à faire un investissement qui fait intervenir des actions d’entreprises cotées et des devises, il a deux façons de faire. Soit il se fie exclusivement au marché qui grâce à ses cotations d’actions, de devises, de matières premières  et de produits à terme sur tous ces actifs lui donne apparemment toute l’information sur les incertitudes du projet. Soit il dépense un budget spécifique pour s’enquérir lui-même de la rentabilité de l’affaire dans laquelle il entend s’impliquer ainsi que ses incertitudes. Cette seconde méthode est « l’ancienne logique économique » qui était la principale façon de faire avant les années 1970, qui consistait à utiliser des experts pour étudier les projets et des ingénieurs pour évaluer les chances de réussites des innovations des entreprises. Cette méthode est plus chère que la première qui est gratuite. Mais elle ne fabrique pas l’information de la même manière. Les deux voies sont d’autant plus différentes que la volatilité est grande.

Pour l’investisseur ne pas utiliser uniquement le marché fournit une information de meilleure qualité. Pourquoi ? Parce qu’elle peut tenir compte de facteurs que le marché ignore, par exemple les liens d’intérêts entre l’investisseur et la région géographique concernée ou encore les catégories de biens dont il est question dans le projet, enfin la qualité des hommes qui pilotent compte tenu des informations recueillies, etc.

---