 Année 1770, point culminant de l’Ancien Régime. Aux sommets de la philosophie et des mathématiques, Kant et Euler vont vers la gloire.
Année 1770, point culminant de l’Ancien Régime. Aux sommets de la philosophie et des mathématiques, Kant et Euler vont vers la gloire.
L’époque bouillonne de penseurs originaux et dissidents, Hume, Adam Smith, Voltaire, Rousseau, d’Alembert, Diderot porteurs d’interrogations nouvelles.
Lavoisier a 27 ans, Lagrange 34,
Louis XVI n’est pas encore sur le trône.
Kant a des idées sur les mathématiques. Dans son système, il leur donne une place exceptionnelle, sur mesure, les jugements synthétiques a priori. Elles nous apprennent quelque chose mais ne tirent pas cette connaissance de l’expérience.
Quant à Euler, il est philosophe à sa manière. Dans les trois volumes des Lettres à une princesse d’Allemagne sur divers sujets de physique et de philosophie, il ne construit pas une métaphysique mais part du concret, à la manière d’Aristote, en mettant à jour la physique dans ses conséquences sur le monde quotidien, la musique et les sons, la chaleur, l’optique, les couleurs, la gravité, les planètes, les marées, il traite de la logique, de l’électricité et décrit les machines qui la fabriquent et la propagent, des longitudes et de la synchronisation des horloges, des aimants et du magnétisme, etc. Ces connaissances lui permettent d’aborder plus constructivement les questions philosophiques importantes que les philosophes abordent avec les seuls moyens d’une intuition pure : l’origine des forces, l’âme et le corps, la liberté, le scepticisme (les Pyrrhoniens), etc.
Une question lui tient visiblement à cœur, c’est la thèse des monades, ce qu’un siècle plus tard on appellera l’hypothèse atomique. Euler n’entre pas dans le système de La Monadologie de Leibniz mais simplement réfute les positions des « monadistes » qui considèrent qu’il y a des petites parties ultimes insécables. Il y consacre dix lettres, quarante pages.
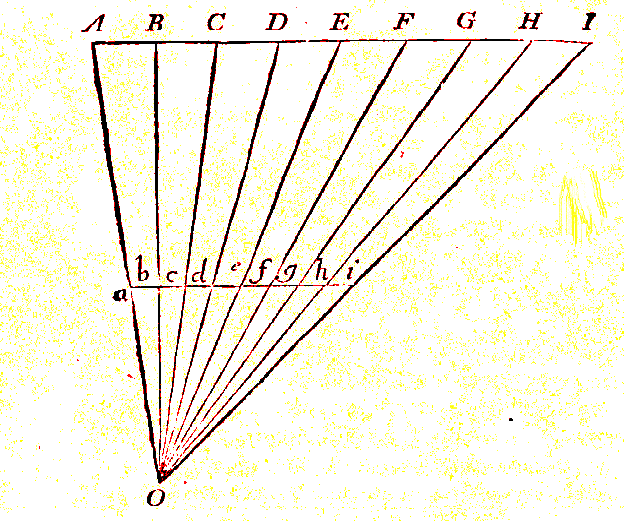
D’abord il montre que la substance en général est divisible à l’infini. Pour diviser un petit segment il se sert de l’homothétie suivant la figure ci-dessus. Puis son argument est le suivant : si les grandeurs géométriques sont divisibles à l’infini c’est qu’il s’agit d’une propriété de la substance en général qui a été tirée de ce qu’elle est une propriété des substances individuelles. Et si cette divisibilité infinie ne s’appliquait qu’à la substance en général en non aux substances particulières on ne l’aurait pas accepté comme propriété de l’étendue en général. « il en est de même que si je voulais dire que l’entendement et la volonté sont bien des attributs de la notion de l’homme en général, mais ne saurait avoir lieu dans les hommes individuels existans. »
La déduction d’Euler est assez curieuse, il révèle d’ailleurs la fragilité de sa propre conviction en invoquant un argument d’autorité : il cite le concours sur cette question lancé en 1748 par l’Académie de Berlin et le prix accordé à M de Justi pour ses arguments contre les monades.
Euler fustige, de longues pages durant, les philosophes qui soutiennent les monades (Lettres CXXIII à CXXXII). Il ne veut pas lâcher sur ce sujet, il n’est pas question pour lui d’accepter un « peut-être, nous ne savons pas » qui serait une position de philosophie et non de science. Il termine la Lettre CXXVII en disant « Aussi les Monadistes redoutent-ils beaucoup cet argument, et ils sont fort indécis, quand on leur demande combien il faut de monades pour produire une étendue ? Il leur semble que deux serait trop peu et ils disent qu’il en faut plusieurs ». Cette pique est amusante quand on pense que c’est bien la détermination approximative du nombre d’Avogadro (J. Perrin et L. Brillouin) qui fut l’argument décisif pour les atomes alors que plusieurs grands savants (Berthelot, Le Chatelier) n’y croyaient pas.
La véhémence et la caricature qu’utilise Euler contre les philosophes atomistes est révélatrice de l’attachement à une interprétation. On ridiculise violemment les hypothèses qui, dans le contexte d’une époque, apparaissent peu vraisemblables.
Je voudrais tenter ici d’approfondir la vision du monde qu’il défend.
Le monde continu et sa cohérence
La vision eulérienne est évidemment largement majoritaire à l’époque, et le restera jusqu’au troisième tiers du 19ème siècle où les polémiques et controverses commencent sérieusement. Elle consiste à considérer que rien ne fait obstacle à ce que l’espace mathématique se prolonge sans fin vers l’infiniment petit pour décrire les corps solides et liquides ainsi que toute la nature. Derrière cette conception il y a toute la cohérence du calcul différentiel, y compris pour les fonctions implicites de plusieurs variables. Le terme de « molécules » employées souvent par les savants du début du 19ème siècle ne signifient pas qu’ils sont atomistes, au contraire cela désigne une partie des corps de dimension arbitraire suffisamment petite pour pouvoir être considérée comme descriptible simplement, ce sont ce qu’on appellerait aujourd’hui des « éléments finis », c’est le langage de Cauchy en mécanique des milieux continus, de Joseph Fourier pour la chaleur, etc.
Même les chimistes restent longtemps opposés à l’hypothèse atomique parce que les proportions définies, en nombres entiers, dans les réactions, ne sont pas incompatibles avec le monde continu. Il suffit d’attribuer aux substances des caractéristiques qualifiées par des entiers, comme on pratique la chimie macroscopiquement, de la même façon que l’espace a des dimensions en nombre entiers jusqu’à trois.
Et la nature naturelle ? Est-ce que les êtres vivants sont des preuves des atomes ? Comment la petite graine de coquelicot peut redonner une plante et sa fleur indéfiniment ? Euler n’en parle pas, il eût été ultra-présomptueux à cette époque de soutenir que la physique pût « expliquer » les êtres vivants. Il invoque souvent Dieu. Mais d’un autre côté, les graines semblent relever d’une question philosophique différente, elles ne se juxtaposent pas en un continuum macroscopique, elles ne sont pas des monades telles qu’Euler les combat.
Le monde continu et les probabilités
Selon toute vraisemblance Laplace partageait le point de vue d’Euler. Lorsque, dans la fameuse préface de sa Théorie analytique des probabilités, il explique que si nous pouvions connaître toutes les forces dont la nature est animée et la situation respective des êtres qui la compose, nous pourrions savoir tous les mouvements jusqu’à celui du plus léger atome, ici encore le terme d’atome se réfère à une toute petite partie. L’usage des probabilités est indispensable, dit-il, parce que nous sommes incapables de mener à bien tous ces calculs.
Mais de quel hasard s’agit-il ? C’est le monde continu qui a été mis en morceaux, brisé en miettes, mélangé, donnant des situations extrêmement compliquées qui nous empêchent d’appliquer les beaux calculs des milieux continus.
Le hasard ici est un hasard qui descend du macroscopique vers le microscopique. Une thèse parfaitement tenable philosophiquement. On peut broyer cette pierre à l’état de sable et les calculs ne seront plus possibles. Mais chaque grain de sable est simple et suit les lois de la mécanique.
Le lecteur voit où je veux en venir. La grande rupture de la physique statistique puis quantique est qu’on admet un hasard qui monte du microscopique vers le macroscopique, et qu’on a trouvé les outils mathématiques et conceptuels pour en parler avec une nouvelle cohérence qui remplace l’ancienne. Le microscopique est créatif de hasard. Il y a de l’indépendance au sens probabiliste dans le microscopique, indépendance qui ne vient pas de procédures macroscopiques. Le calcul des probabilités joint au calcul différentiel classique ne suffisent pas à rendre compte de ce qui monte, les monades s’agitent, on ne peut plus les penser comme les différentielles de Fourier.
Dans la conception d’Euler les petites parties de matière sont passives, elles subissent comme des grains de sable les sollicitations et les chocs. Nous ignorons les données et conditions exactes de leur mouvement mais en première approximation on peut les traiter par petits blocs, même pour un gaz, un petit élément de fluide a sa propre élasticité sa capacité calorifique et des actions et réactions avec ses voisins et c’est ainsi qu’Euler découvre certaines des équations de la mécanique des fluides.
En revanche avec le mouvement brownien des grains de pollen il y a une fièvre même dans un gaz au repos. Et encore plus explicitement avec la mécanique quantique et ses relations d’incertitude. Une précision infinie n’est pas possible parce que le monde microscopique est hasardeux en lui-même. Et ceci a des répercussions macroscopiques. Dans le cas de la turbulence par exemple deux filets voisins de fumée vont évoluer très différemment parce que deux éléments voisins contiennent des hasards indépendants. C’est à dire qu’ils sont corrélés si leur taille est suffisante pour que leur interaction fasse l’objet de moyennes, mais d’autant plus indépendants que leur dimension diminue et relève du cadre quantique.
Euler se battait pour un monde simple. C’est toujours ainsi que procède la science nomologique elle postule un domaine d’application de la loi plus vaste que ce qu’on a constaté. Et les philosophes, Démocrite, Epicure, avec leurs atomes qu’ils n’avaient jamais vus mais juste pensés, ont fourni des matériaux interprétatifs dans l’éventuel pour mieux rendre compte de la complexité.
[ajouté en nov 2019] On m’a posé la question : mais alors que se passe-t-il du côté de l’infiniment grand ? Est-ce que le hasard y monte ou y descend ?
Chez nos aïeux cela résultait directement de la conception du divin. Les Grecs pensaient que les mortels subissaient les volontés et les caprices des Dieux : hasard qui descend. Et ils s’efforçaient de parer à ces incertitudes par la divination et les sacrifices.
Aujourd’hui la question est-elle bien formulée ? Notons que Pascal traite les deux infinis selon deux visions très différentes, de l’infiniment grand il dit peu de choses « une sphère infinie dont le centre est partout et la circonférence nulle part. Enfin, c’est le plus grand caractère sensible de la toute puissance de Dieu, que notre imagination se perde dans cette pensée. » Au contraire il voit l’infiniment petit comme « une infinité d’univers, dont chacun a son firmament, ses planètes, sa terre, en la même proportion que le monde visible; dans cette terre, des animaux, et enfin des cirons, dans lesquels il retrouvera ce que les premiers ont donné; et trouvant encore dans les autres la même chose sans fin… ». Il voit comme sorte d’auto-similarité du côté de l’infiniment petit. Et si on se place en mathématiques, on voit la grande nouveauté qu’apportera Cantor : il ne s’agira plus de similarité, d’homothétie, les profusions ne seront plus comparables.
Mais la question porte sur le hasard. Si on se place en physicien on a tenir compte de ce que les flux d’énergie permettent aux systèmes ouverts une certaine « fantaisie ». Léon Brillouin écrivait en 1959 (quelques années avant les travaux fondateurs de Ilya Prigogine) « La terre n’est pas un système fermé et la vie se nourrit de l’énergie et de l’entropie négative qui pénètre dans le système terrestre. La chaleur du soleil et la pluie font les récoltes. Les récoltes fournissent la nourriture, et le cycle se traduit ainsi : d’abord création d’équilibres instables (combustibles, nourriture, chutes d’eau, etc.) puis utilisation de ces réserves par toutes les créatures vivantes » (Vie matière et observation, Albin Michel 1959). Mais cette « fantaisie » n’est pas du hasard…
En tant que systèmes ouverts à notre échelle nous n’avons que si peu d’influence sur ce qui est grand que la question d’une conséquence qui monte ne se pose pas.
