A plusieurs reprises dans ce blog, j’ai évoqué le philosophe Emile Boutroux, parce qu’il défend une position proche de la mienne pour critiquer la science nomologique uniquement faite de lois plus ou moins bien vérifiées, toujours putatives[1]. Mais il le fait avec de mauvais arguments ce qui est le meilleur moyen d’enfoncer une cause importante.
En particulier il se lance hardiment dans la thèse que les lois pourraient être tout à fait autres que ce qu’elles sont. C’est aussi la thèse que développeront les post-modernes en soutenant que les vérités scientifiques sont socialement construites, mais Boutroux n’évoque pas cette manufacture historique de la connaissance, simplement la pure réflexion philosophique qui nous fait comprendre que ces règles pourraient être différentes.
Pour cela il prend l’exemple de la plus prestigieuse des lois la gravitation. Il écrit « Connus par la seule expérience, les rapports les plus généraux des choses demeurent pour nous, comme disait Newton, radicalement contingents. Pourquoi les corps s’attirent-ils en raison de leur masse et non du carré de leur masse ? C’est là un fait rien de plus. »[2] Je renvoie à l’article de ce blog » une phrase de trop » pour une peinture des conséquences d’une loi qui serait en fonction du carré de la masse.
Je voudrais ici mettre mieux en évidence ce que n’a pas vu Boutroux et sur quoi insiste Henri Lebesgue tout au long d’un livre qu’il a écrit spécialement pour contribuer aux bases de l’enseignement : l’importance de l’additivité et de ce qu’on appelle des « grandeurs mesurables » au sens précis de grandeurs additives. [3]
La longueur d’une courbe est une grandeur additive parce qu’étant partagée en deux la longueur totale sera la somme des longueurs des parties. De même pour l’aire d’une surface, le volume d’un corps. Pour cela il faut que les deux parties ne se recouvrent pas qu’elles soient extérieures l’une à l’autre. Et, là, Lebesgue fait une remarque importante. Si l’on a une grandeur mesurée H d’un corps qui est géométrique, c’est-à-dire qu’elle ne dépend que de sa forme, et si cette grandeur H est additive pour une famille de formes à laquelle appartient le corps, alors les autres grandeurs additives qui mesurent le corps seront proportionnelles à H.
C’est le principe de proportionnalité.
Par exemple si on considère les cylindres droits à base circulaire donnée. La mesure de la hauteur H est additive : pour deux cylindres disjoints la hauteur totale est la somme des hauteurs. Il en résulte que le volume qui est aussi une grandeur additive est proportionnel à la hauteur et de même pour la surface latérale (sans les deux bases du cylindre) qui est aussi additive.
Lebesgue prend un exemple moins trivial : la mesure des angles polyèdres. Un angle polyèdre est « l’ouverture » au centre de la sphère d’une portion de sphère limitée par des plans diamétraux (passant par le centre de la sphère) et, disons, formant une région convexe.[4] Par deux point de la surface de la sphère passent un et un seul plan diamétral, de sorte que le polygone (dont les côtés sont des portions de grands cercles) que forment les plans du polyèdre sur la surface de la sphère peut être partagé par des plans diamétraux en triangles sphériques.
Si le polyèdre a n côtés, on peut partager le polygone en joignant un sommet aux autres en n-2 triangles. Si on note A, B, C, … les angles des dièdres du polyèdre, on voit alors que la grandeur A+B+C+…- (n-2)π est additive : en partageant le polygone en deux polygones 1 et 2 on a
A1+B1+C1+…- (n1-2)π + A2+B2+C2+…- (n2-2)π = A+B+C+…- (n-2)π.
(D’ailleurs si le plan diamétral qui coupe en deux le polyèdre ne passe pas par des sommets du polygone mais coupe les côtés la formule est encore vraie comme on le voit facilement). Cette grandeur est additive donc les autres grandeurs additives attachées à un angle polyèdre lui sont proportionnelles : le volume V de la région de la sphère découpée par le polyèdre et la surface S sur la sphère.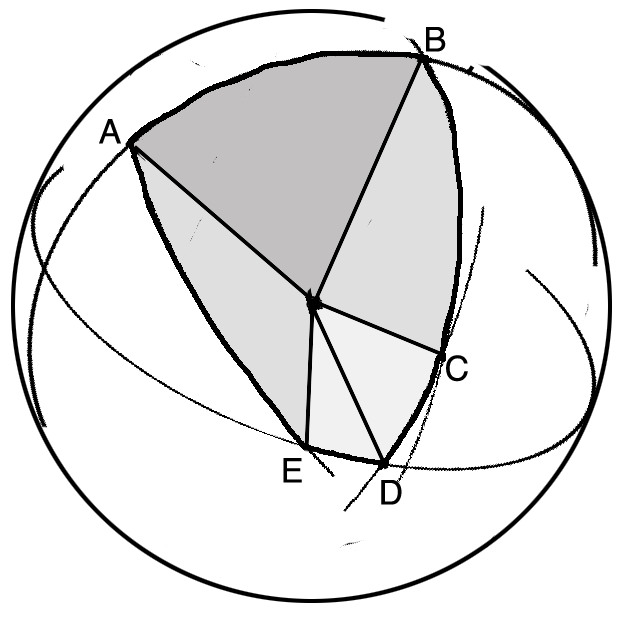 
Pour avoir le coefficient de proportionnalité, il suffit de prendre un cas particulier : celui d’un trièdre trirectangle et on a tout de suite
S = R2 [A+B+C+…-(n-2)p]
V= (R3/3)[ A+B+C+…-(n-2)p]
C’est le théorème d’Albert Girard (1595-1632) mathématicien brillant dont les travaux viennent après ceux de Viète et avant ceux de Fermat et Descartes.
Ce raisonnement fonctionne avec les grandeurs additives comme la masse, la longueur, l’aire, le volume, la chaleur, l’énergie, la charge électrique, etc. Mais non avec les grandeurs telles que densité, température, capacité électrique (sous-additive), etc.
Il faut que les corps de la même sorte qu’on additionne soient extérieurs l’un à l’autre. Mais cette extériorité peut aussi être pensée aussi selon l’axe du temps. L’homogénéité est alors stationnarité. Par exemple le flux solaire est additif dans le temps et l’énergie recueillie par la Terre lui est proportionnelle.
Extériorité dans le domaine des probabilités signifie indépendance. Là ça ne s’additionne pas ça se multiplie. Donc les logarithmes s’additionnent et les diverses notions d’information : de Fisher, de Kullback, de Shannon, de Brillouin font intervenir le logarithme. Les variances aussi s’additionnent.
La question se pose de savoir quel champ de pertinence on peut donner au principe de proportionnalité dans le domaine des probabilités.
Il y a des cas où il s’applique. Par exemple celui du mouvement brownien : ce qui se passe dans deux intervalles de temps disjoints sont des accroissements indépendants, et une translation du temps ne modifie pas les lois conjointes des accroissements. Le temps est une mesure additive pour le mouvement brownien. Donc si on peut trouver une propriété de la trajectoire qui est additive comme la longueur d’une courbe, si le principe s’applique elle sera proportionnelle au temps. Ici la longueur ne marche pas (elle n’existe pas) mais la variation quadratique convient : prise sur deux intervalles disjoints elle s’additionne : donc elle serait proportionnelle au temps. Et c’est le cas. En fait elle est égale à la longueur de l’intervalle sur lequel on la mesure.
[1] Cf. mon livre Science nomologique et science interprétative, connaissance de l’environnement, ISTE 2018.
[2] E. Boutroux De l’idée de loi naturelle dans la science et la philosophie contemporaines (1895).
[3] Henri Lebesgue, Sur la mesure des grandeurs, Gauthiers-Villars, L’Enseignement Mathématique, 1956.
[4] On raisonne donc avec des angles polyèdres dans une demi-sphère, mais comme pour les angles plans l’addition des angles au delà d’un tour complet ne fait pas problème en fait.