Le réductionnisme propose de ramener le monde à l’explication scientifique, quitte à promettre toute la lumière seulement pour demain. Mais on peut voir aussi la science comme fournissant par elle-même des matériaux de réflexion, des exemples de situations, ou de nouage de concepts, qui suscitent le questionnement en partant de la rigueur logique et empirique.
Malgré son titre ce n’était pas ce que faisaient Jean-Pierre Changeux et Alain Connes dans leur célèbre livre Matière à pensée, ils y discutaient plutôt de l’emplacement de nos facultés intelligentes. En revanche c’est vraiment l’esprit de l’œuvre de Jean-Marc Lévy-Leblond à qui je dédie les quelques lignes qui suivent.
Grâce à cet outil curieux et fécond qu’est une théorie scientifique — qui est plus qu’un modèle en ce qu’elle est capable d’en engendrer plusieurs, mais aussi plus spécialisée qu’un langage en ce qu’elle s’appuie sur des paradigmes privilégiés — la science devient un terrain de trouvailles philosophiques. Certaines des configurations qu’elle dessine montrent que le monde n’est pas si simple que l’usage de concepts aux frontières floues pourrait laisser croire.
J’en donne ici quelques exemples.
Le point critique et la fusion faits-valeurs
Le post-modernisme et la sociologie des sciences qui faisaient florès durant les dernières décennies du 20ème siècle commencent à décliner devant les vérités du réel auxquelles l’humanité se cogne. On ressent de plus en plus l’outrance des thèses qui consistaient à tout ramener à des constructions sociales. Non seulement les méthodes et les directions de recherche mais même les contenus de connaissance — notamment les structures — étaient vus comme socialement construits. On dénonçait la coupure moderne et on proclamait la fusion des faits et des valeurs.
On insistait sur le rôle des acteurs et sur les choix en fonction de l’époque, de la culture, des moyens techniques. On soulignait que les dons interprétatifs qui sont mis en œuvre par les savants pour interroger le réel et monter des expériences, sont largement induits par les conditions sociales qui, elles-mêmes, sont le résultat de l’influence d’acteurs politiques ou économiques (stakeholders), qui poursuivent des intérêts particuliers assez différents de ceux des scientifiques « modernes ».
La vision post-moderne, moniste, de la nature qui dénonce la fameuse coupure, est, de fait, beaucoup plus vulnérable à l’emprise économique que la science moderne qui était principalement financée de façon publique. Ainsi le débat se focalise sur les climato-sceptiques qui sont des modernes attardés pour les uns, et pour les autres des activistes habiles à utiliser le social pour semer le doute sur la vérité des mesures et leur interprétation.
Mais la raison philosophique peut-elle sérieusement nous obliger à être soit moniste soit dualiste ?
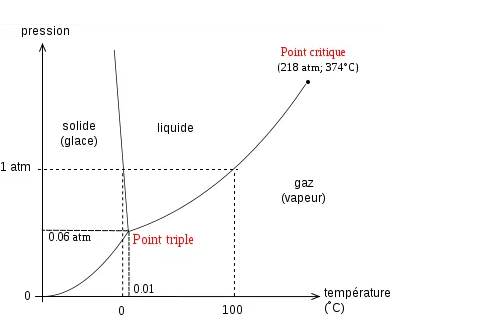
Le diagramme des changements de phase de l’eau est la traduction en volume, température et pression, des divers agencements des molécules d’eau. Autour du point triple apparaissent les phases solide, liquide et gazeuse. Du côté de la phase solide plusieurs configurations cristallines font que certaines glaces sont plus lourdes et d’autres plus légères que l’eau. De l’autre côté une ligne sépare l’état liquide (fortes pressions et basses températures) et l’état gazeux (faibles pressions et hautes températures). A pression constante l’élévation de température effectue un palier lors du franchissement de cette ligne : l’ébullition à température constante.
Mais cette ligne ne va pas au-delà du point de 218 atmosphères et 374 °C., c’est le point critique. On peut dire qu’en deçà du point critique l’eau est « moderne » et au-delà qu’elle est « post-moderne » !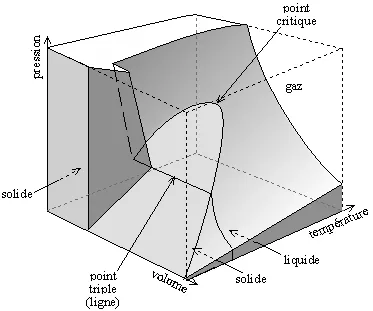 
Le même fluide —ici l’eau — peut passer de façon continue de l’état liquide à l’état gazeux en contournant la ligne qui mène du point triple au point critique, et peut se condenser en gouttelettes à chaque passage de cette ligne sans avoir jamais bouilli.
On peut opter pour une philosophie ni moniste ni dualiste, où la présence d’une coupure dépend des circonstances et des enjeux, mais ne saurait pour autant être effacée. Prenons un exemple.
Le climat est au départ une notion objective, factuelle, caractérisée par les paramètres quantifiant le temps (température, pression, pluviométrie, etc.) dans une certaine région. Dès la Troisième République on a enseigné et on répète aujourd’hui encore qu’il y a des climats suivant les zones, continental, océanique, tempéré, de mousson, etc. Ces idées, comme celles des animaux utiles ou nuisibles, sont des simplifications culturelles et pédagogiques. Aujourd’hui nous voyons les choses plus finement. Les phénomènes météorologiques sont irréguliers, les températures un même jour de l’année varient significativement, variabilité annuelle. Et il y a aussi une variabilité décennale, une variabilité séculaire, et même des tendances millénaires dues notamment aux phénomènes astronomiques, les cycles interglaciaires, etc. Et ces variations à diverses échelles de temps sont, elles aussi, irrégulières. De sorte que la notion de climat devient l’idée qu’il y aurait, malgré les fluctuations, des caractéristiques typiques qu’on obtiendrait, en faisant des moyennes sur suffisamment d’années pour donner des résultats stables, mais non sur des périodes trop longues pour rester dans le domaine de ce qui intéresse les hommes de la génération présente. On voit combien cette notion est tirée de cultures anciennes qui pensaient le monde en régime permanent, et troublé de façon superficielle par des colères passagères des Dieux.
Sur le long terme, les changements ont été considérables, jadis le Sahara fut une mer, et à l’époque historique la région entre le Tigre et l’Euphrate était une riche plaine verdoyante. Le rôle de l’homme dans beaucoup de ces changements est attesté, et les choix techniques furent souvent à courte vue, comme l’assèchement de la mer d’Aral. Donc aussi bien l’homme pourrait être actif pour influencer les choses dans le sens de ce qui, aujourd’hui, compte tenu des savoirs disponibles, semble possible et souhaitable.
On voit alors le climat comme une notion vraiment sociale. D’où l’idée d’Anthropocène, où tout est dans la dépendance de l’homme. Cet homme qui envoie du CO2 qui mange et fait des déchets. Un être vivant qui a besoin pour survivre d’une niche de température et d’hygrométrie, un être sensible aux microbes, etc. C’est là une réalité de faits incontestables. Ces rejets qui changent le climat, il faut les mesurer. Et, pour construire une décision politique cohérente en toute indépendance, capable de résister aux opinions des influenceurs dispersés, et aux intérêts divergents des individus et des groupes, nous avons besoin d’une objectivité reconnue, selon les meilleures méthodes de la science expérimentale.
La boucle est alors bouclée. Nous nous retrouvons de nouveau devant la coupure. La fusion des faits et des valeurs était une solution simplificatrice radicale à un problème mal posé. Le bon schéma est celui d’une ligne de coupure qui s’arrête, ne va pas plus loin. Et l’orientation de la recherche scientifique, le rôle de l’intérêt dans la fabrication de connaissance, la pensée de la technique, forment cette fameuse opalescence autour du point critique.
Les temps exponentiels et la procrastination
Les discours philosophiques sur l’éventualité de l’effondrement se placent toujours au bord du précipice, sans dater précisément l’instant du drame. Les termes de « collapse », « ruine », « désastre » embrassent des phénomènes assez divers, comme l’épuisement des ressources fossiles, le basculement vers un régime climatique irréversible, la mort de beaucoup d’espèces vivantes dans l’océan à cause de son acidification, etc. Il est certain que la signification de l’événement dont on parle est primordiale ainsi que les moyens dont nous disposons pour l’appréhender. Mais nous pouvons simplifier cet événement en le ramenant à une simple date, nous l’appellerons « la catastrophe ».
Ce que les philosophes du catastrophisme n’ont pas vu, ou du moins ce sur quoi ils ont eu tort de ne pas insister, c’est qu’on peut parfaitement croire que la catastrophe est certaine et même proche en un certain sens, sans que ceci, en soi, implique que le temps qui s’écoule sans qu’elle se produise la rende plus imminente. Il est même possible et cohérent que la situation soit parfaitement stationnaire au sens que sa non-survenue jusqu’à présent ne rende la catastrophe ni plus lointaine ni plus proche. Il suffit pour cela de considérer qu’elle survient à un temps aléatoire qui suit une loi exponentielle.
Certains dispositifs sont tels que plus on s’en sert, moins il y a de pannes. Tel le système de reconnaissance vocale de votre téléphone portable parce qu’il est fondé sur l’apprentissage. D’autres mécanismes au contraire s’usent quand on s’en sert, leur panne devient de plus en plus imminente. Mais pour la faillite d’une entreprise par exemple, en première approche, l’économie va prendre simplement le modèle intermédiaire où il n’y a ni apprentissage ni vieillissement. C’est le paradigme de l’imminence constante.[1]
C’est extrêmement courant et banal. Les situations que j’évoque, d’imminence constante, incitent évidemment à ne pas changer de comportement, c’est-à-dire au business as usual. Elles se rencontrent partout dans la vie quotidienne et souvent en physique. Elles sont la base de la représentation des pannes par les ingénieurs. Elles sont la notion la plus simple pour des dispositifs dont la sûreté et la fragilité ne sont pas affectées tant qu’il n’y a pas de panne. Si la catastrophe est déclenchée par la première apparition d’un phénomène parmi un très grand nombre de phénomènes indépendants, elle est d’imminence constante. Si deux ou plusieurs catastrophes indépendantes sont d’imminence constante, la première qui survient est elle-même d’imminence constante. Dans une situation à risque, un signe avant-coureur ne fournit pas généralement de date butoir, de sorte que la constance de l’imminence ne se trouve pas réfutée par un tel avertissement. En général, la causalité entre le signe avant-coureur et la catastrophe est de nature sémantique et ne permet pas une quantification précise
Il y a donc une légitimité à penser que les menaces environnementales même les plus graves se produisent de façon certaine à une date finie aléatoire et soient néanmoins d’imminence constante. Cette vision, si on l’adopte, revient à dire aux écologistes : « causez toujours, ce que vous dites ne change en rien ma situation décisionnelle », plus précisément ma situation pour les décisions économiques. Ajoutons que, pour tenir cette position, il n’est pas nécessaire de connaître le paramètre de la loi exponentielle qui gère ladite catastrophe.
La catastrophe pensée économiquement apparaît donc comme une explication du business as usual, car elle accorde un rôle central – comme schéma mental – aux situations d’imminence constante. Quand Madame et Monsieur Toulemonde vont à la banque placer leurs économies, on leur explique en premier lieu que les placements sûrs ont des rendements bas et que pour avoir des rendements élevés il faut prendre des risques. Dans l’utilitarisme quotidien, le modèle de base est que la faillite de l’entrepreneur, le risque de défaut de n’importe quel prêt se traduit implacablement sur le taux. Et derrière cette « loi » se trouve évidemment la logique que la représentation la plus simple d’une échéance aléatoire est une variable exponentielle, dont le paramètre génère le taux du prêt. Plus c’est risqué, plus l’imminence (constante) est brève, plus le taux est élevé. Et, a contrario, plus c’est confiant et sûr, plus l’imminence (constante) du défaut est lointaine et plus le taux est bas.
Pour résumer, l’économie – et particulièrement la finance de la période néolibérale actuelle –, a installé, avec la pédagogie redoutablement efficace des moyens d’agir, une logique économique où les risques sont – en premier lieu – pensés selon des situations immuables tant que la catastrophe ne s’est pas produite.
L’incomplétude et l’ignorance définitive
Il a été démontré au début des années 1930, sous des formes voisines, par Kurt Gödel, Alonzo Church, et Alan Turing, que l’arithmétique est incomplète.
Explicitons un peu. Il s’agit de l’arithmétique axiomatisée par Peano avec huit axiomes qui définissent l’addition et la multiplication des nombres entiers et l’axiome d’induction qui formalise le raisonnement par récurrence. Il fut prouvé que certains énoncés sont indécidables, ni démontrables ni réfutables, on en a écrit explicitement. Plus généralement les théories non contradictoires qui contiennent l’arithmétique sont incomplètes. Une autre façon d’aborder cette découverte est de considérer la notion d’algorithme c’est-à-dire de procédé permettant de calculer une fonction d’entiers à valeurs entières n=f(m) en un nombre fini d’étapes élémentaires (dépendant de m). L’incomplétude de l’arithmétique peut alors se dire en termes de recherche de démonstrations, ce qui est l’activité du mathématicien et aussi de l’étudiant qui résout un exercice. Les énoncés d’arithmétique sont des formules correctement écrites pour la syntaxe logique. On peut les numéroter de façon effective. Et les démonstrations sont des suites finies d’énoncés conformes à la déduction logique à partir des axiomes, on peut aussi les numéroter de façon effective. Un trait lié à l’incomplétude est que la recherche de démonstration est un problème qui dépasse ce que sait faire un algorithme.
La technicité de ces questions a fait que les philosophes en ont parlé à partir d’informations de seconde main, et que les mathématiciens sont si passionnés par le sujet qu’ils l’ont rendu encore plus technique avec le problème P=NP et d’autres conjectures irrésolues. Or l’incomplétude a des conséquences fondamentales sur les bases de notre éthique scientifique.
Un point fondamental à souligner dans la phénoménologie de l’incomplétude est qu’une démonstration mathématique peut engendrer un énoncé simple à partir de détours par des énoncés très complexes. Et inversement si on se donne un énoncé, la longueur des démonstrations qu’il faut essayer pour le prouver n’a pas de borne effective à partir de la longueur de l’énoncé. Les détours sont plus féconds que les approches directes. Ce phénomène vaut pour les propriétés des nombres entiers mais aussi plus généralement pour tout ce qui concerne la combinatoire à un certain niveau de complexité. Les chimistes s’en étaient rendu compte à propos de la synthèse chimique. Souvent la synthèse d’un corps demande des excursions passant par des corps beaucoup plus compliqués que le produit cible.[2]
Une autre façon d’énoncer ces résultats, celle retenue par Pierre Samuel, est de dire qu’il n’existe aucune théorie axiomatique qui fournisse la totalité des propriétés des nombres entiers. Cela veut dire que les nombres entiers nous réservent des surprises, du côté des grands nombres évidemment. Depuis les années 1930 bien des avancées ont été faites qui ont fourni un grand nombre de problèmes formels ayant cette propriété de dépasser la complexité de l’algorithme. En général ceci est établi par un procédé qui utilise une traduction vers l’arithmétique ou un raisonnement de point fixe comme celui employé par Gödel. On peut penser cependant que les cas où une telle démonstration est disponible sont beaucoup moins nombreux que ceux qui dépassent l’algorithmique sans qu’on puisse à ce jour le démontrer.
Le réductionnisme se voit donc attribuer des bornes strictes. Dire que le complexe engendre du simple c’est dire, dans le domaine de la combinatoire, que le simple est « à la merci » de ce qui se passe dans les régions complexes.
Le contexte a son importance même en ce qui concerne la combinatoire.
Pour les êtres vivants qui sont en coévolution, le contexte a une importance cruciale qui fait intervenir la notion d’écosystème. C’est une dimension sur laquelle la théorie de Darwin n’insistait pas assez. Mais nous voyons que ceci n’est pas réservé au vivant, car la combinatoire elle-même a cette vertu extraordinaire de dépendre de détours par le complexe pour créer des combinaisons simples.
Cela remet en cause un pilier de la philosophie empirique classique. Notamment l’idée qu’il est loisible d’essayer pour voir. Et nous voyons au contraire que penser la nature comme un champ d’expérience librement ouvert à qui veut essayer est une grave erreur fondée sur des croyances religieuses transposées implicitement vers la science.[3]
Retournement d’un processus de Markov et évolution
Par rapport à la théorie de Darwin, la vision contemporaine de l’évolution met davantage l’accent sur les phénomènes collectifs, les écosystèmes, les chaines trophiques, et —évidemment — les organismes microscopiques qui n’étaient pas connus à l’époque. Mais néanmoins le schéma de rationalité générale qui orchestre toute cette symphonie suit une logique dans laquelle ce qui se passe l’instant suivant dérive de ce qui est actuellement.
C’est une sorte de méta-principe méthodologique. Ensuite, diverses stratégies ont été imaginées pour palier le fait qu’on ne sait pas très bien ce qui se passe actuellement. Laplace proposa d’utiliser le calcul des probabilités et cette idée eut un sillage immense, qui règne encore chez les biologistes aujourd’hui comme une évidence qui mérite d’être repensée. Une autre stratégie a consisté à ne porter son regard qu’aux conséquences de ce que l’on peut connaître par l’observation et la mesure, quitte à accepter que « conséquence » soit entendu au sens probabiliste parmi un ensemble de possibles.
Le fait que ce soit le présent qui détermine — éventuellement sous forme de tirage aléatoire — ce qui va se passer est ce qu’on appelle en mathématique un modèle markovien. Au sens strict un tel modèle ne s’appliquerait à l’évolution que si nous étions capables de connaître et de représenter toute la nature à l’état présent. Néanmoins c’est bien cette idée qui est présente dans l’esprit des biologistes lorsqu’ils cherchent à déterminer un dernier ancêtre commun à tout le règne vivant (LUCA), supposant implicitement qu’on va vers du plus simple en remontant le temps.
La bonne méthode serait alors de se servir des probabilités des causes. C’est ce point que je souhaite approfondir un peu. A l’époque de Bayes (1701-1761) tout est simple et discret. D’ailleurs on ne trouve pas la fameuse formule de la probabilité des causes
dans l’œuvre de Thomas Bayes, il semble que cette attribution lui fut faite dès le 18ème siècle. Mais aujourd’hui pour la question de la probabilité des causes nous disposons de davantage d’outils mathématiques. Et il se pose le problème suivant :
Etant donné un processus de Markov de probabilité de transition P, trouver le processus «dual» qui remonte le temps.
Sans entrer dans les détails, il me semble intéressant de remarquer que ceci ne peut se faire que si on se donne la mesure par rapport à laquelle on retourne le processus. La seule donnée de la probabilité de transition ne suffit pas. Le retourné dépend de la mesure choisie. Et il ne sera markovien que si la mesure a certaines propriétés spécifiques comme d’être invariante par P.
Autrement dit l’état présent du système, et la loi de son évolution ne suffisent pas à déterminer les probabilités du système des causes. Pour pouvoir remonter le temps au sens d’une évolution à rebours il faudrait disposer de l’ensemble des états que le réel occuperait selon l’évolution en temps croissants en plus du réel particulier que nous observons.
Cette remarque rejoint d’ailleurs le fait qu’il est d’usage aujourd’hui d’appeler méthodes bayésiennes des approches statistiques qui supposent une probabilité a priori.
Par exemple soit un mouvement brownien en dimension 1 partant de x0. A l’instant t il est au point Xt(w). Connaissant ce point et la probabilité de transition P je ne peux en aucun cas retrouver x0.
La croyance à une simplification des êtres vivants lorsqu’on remonte le temps vient de ce qu’on considère que le système, en temps croissant, est divergent dans les états qu’il prend. S’il est dans l’état précis Xt(w) à l’instant t, alors les naturalistes supposent en général que la probabilité de transition le met dans des états qui dépendent de Xt(w) mais sont tous différents de ceux issus de Xt(w’). Autrement dit les trajectoires du processus ne se coupent pas. C’est tout à fait imaginable si la dimension de l’espace est infinie comme c’est le cas s’il s’agit d’un univers de formes.
Ceci est une amorce d’une discussion qui pourrait aller beaucoup plus loin. Je veux juste souligner une faiblesse de ce genre d’argumentation qui consiste à utiliser la notion d’état du « système nature » et de lui appliquer des propriétés probabilistes alors que cet « état de la nature » nous ne le connaissons pas et nous ne le connaitrons jamais dans tous ses détails tant le microscopique est abondant, varié, et changeant, question d’ordres de grandeur.
Ces exemples sont significatifs, ils témoignent parmi une multitude de cas d’une certaine image du réel fournie par la science : elle est méthodologiquement réductionniste, mais ne fournit que des rationalités partielles, des schèmes déductifs non connectés entre eux. On ne sait pas retrouver le diagramme des phases de l’eau à partir de l’équation de Schrödinger de la molécule d’eau, sauf à faire intervenir de nouvelles informations.
Ces schèmes ont des allures de théories et poussent en se ramifiant comme des arbres. Ils ne sont pas simplement posés les uns à côté des autres mais suivent aussi des contraintes communes comme une forêt.
Par rapport à ce qu’il faut bien appeler la religion scientiste, philosophie de Ernst Haeckel (1834-1919) par exemple, où l’on rêve de tout embrasser dans une seule déduction rationnelle, cela accorde un rôle créatif aux combinaisons de facteurs extérieurs éloignés jusqu’à l’infini qui nous imposent d’admettre une ignorance en permanence présente, non pas comme quelque chose que nous pouvons oublier mais comme un creuset qui fait apparaître du nouveau parfois favorable parfois dangereux…
[1] Les détails mathématiques sont très simples. Un événement de date T > 0 est d’imminence constante si
alors on a toujours
Donc le fait que T ne soit pas survenue à l’instant s ne change pas la loi de la durée à attendre encore. C’est comme si le fait que l’événement ne se soit pas produit à l’instant s, n’était pas une information. Cf. N. Bouleau Processus stochastiques et application, Paris, Hermann 2000, p. 82 sq.
[2] Cf. N. Bouleau, Ce que Nature sait, PUF 2021, chapitre 2, à propos des travaux de Roald Hoffmann notamment.
[3] Je renvoie pour les approfondissements de ce paradigme au livre à paraître N. Bouleau et D. Bourg Science et prudence, Réductionnisme et autres erreurs par gros temps écologique, PUF, juin 2022.