Deux sortes de beauté

Christopher Wren et Claude Perrault

« Il y a deux origines à la beauté : naturelle et coutumière. La naturelle vient de la géométrie, elle consiste en uniformité (c’est-à-dire égalité) et en proportion. La beauté coutumière est le résultat de notre perception des objets qui nous sont ordinairement agréables pour d’autres raisons, la familiarité ou l’inclination pouvant faire naître l’amour pour des choses qui ne sont pas aimables en elles-mêmes. »

Ainsi s’exprime, vers la fin du dix-septième siècle, Christopher Wren, architecte de la cathédrale Saint Paul de Londres dans ses Tracts on Architecture traité inachevé, synthèse de sa longue expérience de constructeur. L’homme est non seulement l’architecte le plus renommé d’Angleterre à l’époque, mais savant reconnu, président de la Royal Society, correspondant de John Wallis et d’Isaac Newton. Né sous le règne de Charles 1er en 1632, il consacre sa jeunesse, durant la dictature de Cromwell, aux mathématiques. On lui doit un calcul de la longueur d’un arc de cycloïde par une méthode apparentée à celle des « indivisibles » de Cavalieri et Roberval. Il fut professeur d’astronomie à Londres puis à Oxford et membre de la Royal Society dès 1662. A l’âge de trente ans, il a déjà contribué aux débats scientifiques autour de la troisième loi de Kepler et de l’attraction en 1/r². Puis il s’est tourné vers l’architecture, sa véritable passion, pour laquelle il n’avait pas de formation particulière si ce n’est cette solide culture scientifique, tant mathématique que mécanique.

Il peut sembler curieux que la beauté géométrique soit qualifiée de naturelle par Wren. De même que pour la célèbre toile du Titien, quelle femme exprime l’amour sacré plutôt que profane ?

Comme ses contemporains, Descartes en particulier, il classe la géométrie dans la beauté donnée par la nature et oppose à celle-ci ce qui relève des sens et de la société sans toutefois mépriser ce second volet, point intéressant de sa doctrine. Cette opposition fondamentale de l’architecture est pour Wren une source d’inspiration. D’un côté « l’architecture vise l’éternité » et donc doit s’appuyer sur les « ordres » (dorique, ionique, corinthien) qui sont en dehors des courants et des modes. D’un autre côté il accepte l’ordre « composite » et insiste sur l’importance des ordres phénicien, hébreu, et assyrien, et sur l’expérience de « toutes les époques ». D’une part il écrit « les figures géométriques sont naturellement plus belles que les autres irrégulières, c’est une loi de la nature. Parmi les figures géométriques, le carré et le cercle sont les plus belles, puis le parallélogramme et l’ovale » comme Le Corbusier écrira dans son manifeste Vers une architecture : « les cubes, les cônes, les sphères, les cylindres ou les pyramides sont les grandes formes primaires que la lumière révèle bien […] C’est pour cela que ce sont de belles formes, les plus belles formes ». D’autre part Wren est conscient de la socialité de l’acte de construire : « L’architecture a un rôle politique; les constructions publiques sont l’ornement du pays, elle est le fondement de la nation, elle tire le peuple et le commerce et fait aimer son pays au peuple. » L’architecture est édifiante aux deux sens du terme. Elle doit aussi être commode, s’accorder avec les besoins et le nombre des usagers.

La dualité pointée par Christopher Wren est une problématique permanente et fondamentale de l’architecture qui se retrouve sous diverses variantes à toutes les époques. Alberti sépare l’harmonie intrinsèque due aux proportions et l’ornementation. Pour Palladio « la beauté résulte de la forme et de la correspondance du tout aux parties, des parties entre elles et de celles-ci au tout de sorte que l’édifice apparaisse comme un corps entier et bien fini dans lequel chaque membre convient aux autres et où tous les membres sont nécessaires à ce qu’on a voulu faire ». Et tous deux se réfèrent à Vitruve qui enseigne que la valeur d’un édifice tient autant à l’ordonnance qu’à la commodité.

Si les idées de la Renaissance, florissantes en Italie dès le quinzième siècle, ont conquis la France au seizième et l’Angleterre au dix-septième, comme possibilités créatives nouvelles, elles risquent aussi d’installer des « manières ». La géométrie à cet égard efface les appartenances, les styles, par sa perfection universelle elle émancipe des ordres et des imitations. Mais peut-on vivre dans un cube, une sphère ou autre forme simple ? Ce n’est réellement envisageable que pour le séjour éternel d’un Pharaon. La modénature, les corniches, balustres, corrections de perspective ou d’échelle sont un superflu indispensable. Les décors grotesques inspirés des fresques romaines se répandent dans les palais et seront l’engouement de toute l’Europe au dix-huitième siècle. L’esprit de géométrie alterne avec l’esprit de finesse.

Contemporain de Wren, l’architecte français Claude Perrault est lui aussi un savant reconnu et académicien. Il a traduit et annoté Vitruve et a publié une Ordonnance des cinq espèces de colonnes selon la méthode des anciens qui sera lue comme un traité du classicisme français. Perrault partage avec Wren une conception duale de la beauté : il distingue les « beautés positives » et les « beautés arbitraires », ce qui émane probablement de sa formation de physiologiste et de son œuvre dans les sciences naturelles où il s’est frotté aux difficultés de l’expérimentation. Les deux sortes de beauté chez Perrault s’apparentent à l’opposition entre le fait et le droit : »les beautés positives semblent se rapporter à la structure intrinsèque de l’édifice, tandis que les beautés arbitraires concernent plutôt son fonctionnement à l’intérieur du système du goût ».[1]

Bien avant que les historiens et théoriciens de l’architecture ne plaquent sur la problématique architecturale la grille de la linguistique avec syntaxe et sémantique (cf. Ch. Norberg-Schulz, M. Tafuri, etc.), Perrault et Wren sentent l’analogie de la dualité du beau avec le langage régi par des règles et compris par l’usage. « La variété des uniformités fait la complète beauté, écrit Wren, les uniformités doivent être tempérées, comme les rimes en poésie, parfois alternées, parfois avec plus de variété comme dans les stances ». Il y a donc une langue à apprendre, pour dire grâce à elle les plus belles choses. Wren entreprend en 1665 un voyage à Paris, de même que l’usage se rependait parmi les architectes français de parfaire leurs connaissances en Italie.[2]

Wren à Paris

Armé de lettres d’introduction, notamment auprès du Comte de St Albans, Wren rencontre les grands architectes du moment et visite nombre d’églises, de palais et de chantiers dans la ville et les environs. Il est impressionné par l’abondance des projets et l’activité de la vie parisienne. « Les femmes, qui font ici le langage et la mode, et se piquent de politique et de philosophie, écrit-il à un ami, font aussi la loi en architecture : les ouvrages en filigrane et autres petites fantaisies sont grandement en vogue. Pourtant la construction devrait revêtir les attributs de l’éternité, et donc être le seul objet incapable de modes nouvelles ». Il rencontre François Mansart et Louis Le Vau, visite l’église du Val de Grâce encore en travaux, et celle de la Sorbonne achevée par Jacques Lemercier quelques années auparavant qui l’impressionne grandement. Il s’en inspirera pour la cathédrale St Paul sur laquelle il avait commencé à réfléchir dès 1661[3]. Christopher Wren se trouve à Paris juste au moment du court séjour du Bernin en France. Appelé par Colbert, celui-ci était venu parachever le palais du Louvre vers l’Est. Mais le prodige italien, capable de création en sculpture et en architecture à la hauteur de Michelange et de Palladio, est l’objet de jalousies et les intrigues diverses feront échouer ses propositions, Perrault principal instigateur de ces querelles réalisant finalement la fameuse colonnade avec ses doublons de colonnes à laquelle son nom reste attaché.[4]

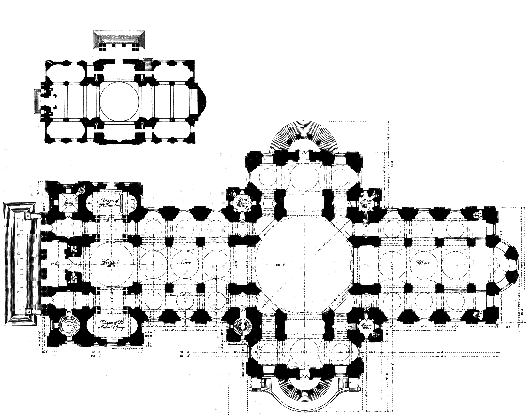
Plans de St Paul et de l’église de la Sorbonne construite de 1635 à 1655 par Jacques Lemercier. Elle fut visitée par le Bernin qui en fit quelques critiques ainsi que par Wren qui fut impressionné et repris la symétrie du plan pour St Paul.

Le souci premier de Wren est de ramener de Paris, des dessins, des croquis et des gravures sur des œuvres récentes. Il parvient à rencontrer le « cavalier » Bernin. « J’aurais donné ma peau, écrit-il à son ami, pour avoir les projets du Bernin pour le Louvre, mais ce vieil Italien secret ne me les laissa voir que quelques minutes. Il y avait là cinq petits dessins sur papier, pour chacun desquels il a touché mille pistoles. J’ai seulement eu le temps de les copier dans ma mémoire ». Mais pour alimenter son imagination sous le registre de la beauté coutumière, Wren fait aussi les marchands d’estampes : « J’ai acheté grand nombre de tailles douces, afin de donner à nos compatriotes des exemples d’ornements et de grotesques, pour lesquels les Italiens eux-mêmes reconnaissent que les Français sont insurpassables »

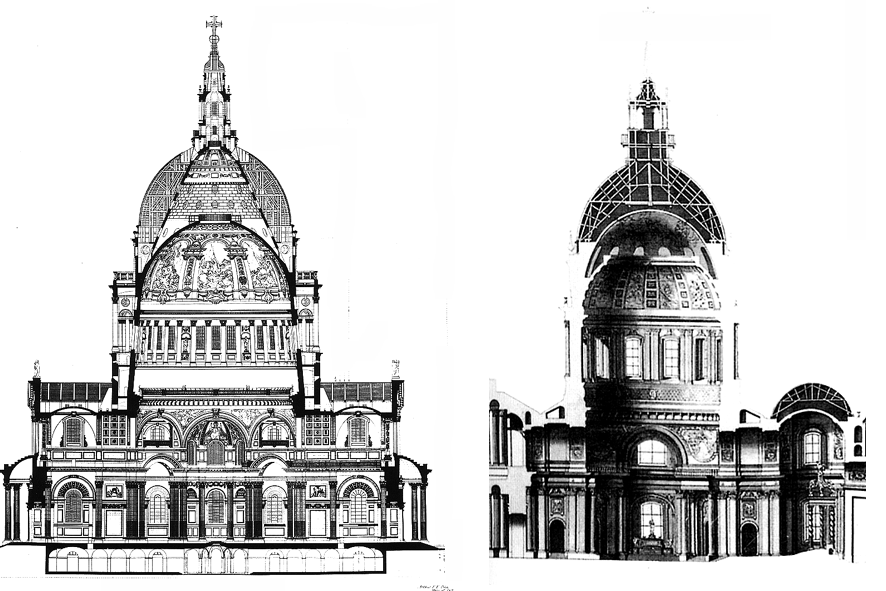Coupes de la cathédrale St Paul (à g.) et de l’église royale des Invalides (à d.) construites l’une par Christopher Wren de 1675 à 1708 l’autre par Jules Hardouin-Mansart de 1677 à 1706.

On ne sait si Wren a rencontré Jules Hardouin-Mansart qui réalisera l’église des Invalides exactement pendant que Wren édifiera St Paul. Les deux dômes ont en commun de posséder trois coupoles, la plus extérieure soutenue par la charpente, la plus intérieure décorée de fresques et une intermédiaire, originale, de fonction différente dans les deux édifices. En revanche une source d’inspiration certaine pour St Paul est la basilique St Pierre de Rome dont Wren a pu voir l’une des versions de Bramante ou même l’un des projets de façade par le Bernin lui-même.

La gravure montre le projet de façade de St Pierre de Rome avec des tours aux angles proposé par le Bernin et jamais réalisé pour cause de fondations insuffisantes. Wren rencontra le Bernin à Paris qui lui montra quelques uns de ses projets pour le Louvre. A droite la façade de St Paul.

Après l’incendie de Londres

Wren est de retour en mars 1666, et assiste, impuissant comme tous les londoniens, à l’incendie violent qui ravage la ville en septembre de la même année. La reconstruction s’organise. Si ses plans d’urbanisme ne sont finalement pas retenus, il est en revanche chargé non seulement de la construction de la nouvelle cathédrale, mais de superviser la réalisation de 50 églises à Londres et aux alentours, tâche où son talent et toute la dialectique subtile sur laquelle il a médité, entre le nécessaire et le fortuit, entre la géométrie et l’ornement, seront mis en œuvre. La variété de ces églises est telle qu’elle a été comparée à celle des villas de Palladio. Wren est, en effet, un siècle après le grand « compositeur » de Vénétie, créateur d’un langage nouveau. Le registre est cependant différent, il pointe dans le style de Wren une certaine ironie critique, des juxtapositions et des proportions inhabituelles, voire cocasses, qui préfigurent l’hétéroclite et les catégories ambiguës (both-and, double-functioning element) dont Robert Venturi se fera le chantre au vingtième siècle et où se reconnaîtront les post-modernes.[5]

La dernière église dessinée et construite par Christopher Wren est St Stephen à Walbrook près de la Tamise.

Eglise St Stephen dans le quartier Walbrook de Londres. Une des plus émouvante réussite de Wren. L’église est rectangulaire à coupole centrale sur base octogonale. Le bas côté est à la nef dans le rapport 1/√2. La savante transition de la coupole au réseau des colonnes qui permet un jeu de lumière et d’ombres a été comparée par R. Venturi a une trouvaille analogue dans un palais de Borromini.

Petite merveille de géométrie, elle atteint cette cristallisation remarquable que les théoriciens de l’Antiquité et de la Renaissance désignaient sous le terme d’ordonnance. Comparée à juste titre à la chapelle Pazzi de Brunelleschi à Florence, elle a cette perfection ordinaire, simple et complexe à la fois, unique dans son plan et sa volumétrie, baignée de lumière naturelle, sans vitraux, chargée d’un décor discret et comme évident, elle dégage une mystérieuse harmonie qui élève l’esprit vers dieu grâce aux mathématiques. Les deux sortes de beauté s’y répondent parfaitement comme, dans une fugue, le mouvement principal et le phrasé mélodique.

Chapelle Pazzi de Brunelleschi à Florence, perle de la première Renaissance italienne.

 

[1] A. Picon, Claude Perrault, la curiosité d’un classique, Picard 1988.

[2] C’est ce qu’avait fait déjà l’architecte Inigo Jones (1573-1652) Qui fit connaître Palladio en Angleterre.

[3] Il rencontre également le mathématicien et architecte Guarino Guarini qui est à Paris de 1661 à 1666 pour le chantier de l’église Ste Anne-la-Royale du couvent des théatins qui restera inachevée.

[4] La paternité de Claude Perrault sur cette colonnade reste aujourd’hui objet de controverse. Cf. A. Picon op. cit. En plus des colonnes jumelées, Perrault est l’inventeur d’un chapiteau nouveau pourvu de plumes au lieu de feuilles d’acanthe, tenues par un cercle de fleurs de lys.

[5] R. Venturi, auteur du « gentle manifesto » Complexity and contradiction in architecture,( Museum of modern Art, 1966) a réalisé l’extension récente de la National Gallery à Londres.